Approaching ...
- 1.3 Limits Graphical And Analytical Connectionsap Calculus Solution
- 1.3 Limits Graphical And Analytical Connectionsap Calculus Answers
- 1.3 Limits Graphical And Analytical Connectionsap Calculus Pdf
- 1.3 Limits Graphical And Analytical Connectionsap Calculus Solutions
- Perhaps not, but there is likely a limit that we might describe in inches if we were able to determine what it was. To put it mathematically, the function whose input is a woman and whose output is a measured height in inches has a limit. In this section, we will examine numerical and graphical approaches to identifying limits.
- F x x3 x2 x 1 x 1 3 f(x) = 2, x ≠ 3 0, x = 3 x y −112 4 −1 1 3 4 Figure 11.6 Some students may come to think that a limit is a quantity that can be approached but cannot actually be reached, as shown in Example 4. Remind them that some limits are not.
AP Calculus I Notes 2.3 Evaluating Limits Analytically In some cases, the limit can be evaluated by direct substitution. Lim ( ) xc fx o iff fx is. Theorem – Some Basic Limits Let b and c be real numbers, and n be a positive integer. 1) lim xc b o lim 2) lim xc x o 3) n xc x o Ex. 1: Find each limit: a) 2 lim3 xo b) 4 lim x x o c) 2 3 lim. 1.3 Estimating Limit Values from Graphs. LEARNING OBJECTIVE. LIM-1.C Estimate limits of functions. LIM-1.C.1 The concept of a limit includes one sided limits. LIM-1.C.2 Graphical information about a function can be used to estimate limits. LIM-1.C.3 Because of issues of scale, graphical representations of functions may miss important function. Graphical Approach to Limits. Example 3: The graph below shows that as x approaches 1 from the left, y = f(x) approaches 2 and this can be written as lim x→1-f(x) = 2 As x approaches 1 from the right, y = f(x) approaches 4 and this can be written as lim x→1 + f(x) = 4 Note that the left and right hand limits and f(1) = 3 are all different.
Sometimes we can't work something out directly ... but we can see what it should be as we get closer and closer!Example:
(x2 − 1)(x − 1)
Let's work it out for x=1:
1.3 Limits Graphical And Analytical Connectionsap Calculus Solution
(12 − 1)(1 − 1) = (1 − 1)(1 − 1) = 00
Now 0/0 is a difficulty! We don't really know the value of 0/0 (it is 'indeterminate'), so we need another way of answering this.
So instead of trying to work it out for x=1 let's try approaching it closer and closer:
Example Continued:
| x | (x2 − 1)(x − 1) |
| 0.5 | 1.50000 |
| 0.9 | 1.90000 |
| 0.99 | 1.99000 |
| 0.999 | 1.99900 |
| 0.9999 | 1.99990 |
| 0.99999 | 1.99999 |
| ... | ... |
Now we see that as x gets close to 1, then (x2−1)(x−1) gets close to 2
We are now faced with an interesting situation:
- When x=1 we don't know the answer (it is indeterminate)
- But we can see that it is going to be 2
We want to give the answer '2' but can't, so instead mathematicians say exactly what is going on by using the special word 'limit'.
The limit of (x2−1)(x−1) as x approaches 1 is 2
And it is written in symbols as:
limx→1x2−1x−1 = 2
1 x^2~−1/x−1 = 2 -->So it is a special way of saying, 'ignoring what happens when we get there, but as we get closer and closer the answer gets closer and closer to 2'
As a graph it looks like this: So, in truth, we cannot say what the value at x=1 is. But we can say that as we approach 1, the limit is 2. |
Test Both Sides!
1.3 Limits Graphical And Analytical Connectionsap Calculus Answers
It is like running up a hill and then finding the path is magically 'not there'...
... but if we only check one side, who knows what happens?
So we need to test it from both directions to be sure where it 'should be'!
Example Continued
So, let's try from the other side:
| x | (x2 − 1)(x − 1) |
| 1.5 | 2.50000 |
| 1.1 | 2.10000 |
| 1.01 | 2.01000 |
| 1.001 | 2.00100 |
| 1.0001 | 2.00010 |
| 1.00001 | 2.00001 |
| ... | ... |
Also heading for 2, so that's OK
When it is different from different sides
How about a function f(x) with a 'break' in it like this:
The limit does not exist at 'a'
We can't say what the value at 'a' is, because there are two competing answers:
- 3.8 from the left, and
- 1.3 from the right
But we can use the special '−' or '+' signs (as shown) to define one sided limits:
- the left-hand limit (−) is 3.8
- the right-hand limit (+) is 1.3
And the ordinary limit 'does not exist'
1.3 Limits Graphical And Analytical Connectionsap Calculus Pdf
Are limits only for difficult functions?
Limits can be used even when we know the value when we get there! Nobody said they are only for difficult functions.
Example:
limx→10x2 = 5
10 x/2 = 5 -->We know perfectly well that 10/2 = 5, but limits can still be used (if we want!)
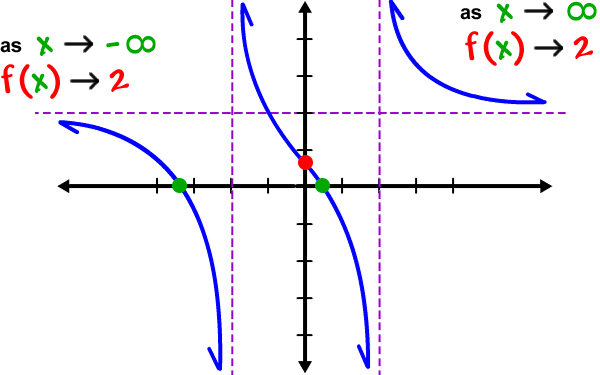
Approaching Infinity
Infinity is a very special idea. We know we can't reach it, but we can still try to work out the value of functions that have infinity in them.
Let's start with an interesting example.
| Question: What is the value of 1∞ ? |
| Answer: We don't know! |
Why Don't We Know?
The simplest reason is that Infinity is not a number, it is an idea.
So 1∞ is a bit like saying 1beauty or 1tall.
Maybe we could say that 1∞= 0, ... but that is a problem too, because if we divide 1 into infinite pieces and they end up 0 each, what happened to the 1?
In fact 1∞ is known to be undefined.
But We Can Approach It!
So instead of trying to work it out for infinity (because we can't get a sensible answer), let's try larger and larger values of x:
| x | 1x |
| 1 | 1.00000 |
| 2 | 0.50000 |
| 4 | 0.25000 |
| 10 | 0.10000 |
| 100 | 0.01000 |
| 1,000 | 0.00100 |
| 10,000 | 0.00010 |
Now we can see that as x gets larger, 1x tends towards 0
We are now faced with an interesting situation:
- We can't say what happens when x gets to infinity
- But we can see that 1x is going towards 0
We want to give the answer '0' but can't, so instead mathematicians say exactly what is going on by using the special word 'limit'.
The limit of 1x as x approaches Infinity is 0
And write it like this:
limx→∞1x = 0
INF 1/x = 0 -->In other words:
As x approaches infinity, then 1x approaches 0
It is a mathematical way of saying 'we are not talking about when x=∞, but we know as x gets bigger, the answer gets closer and closer to 0'.
Read more at Limits to Infinity.
Solving!
We have been a little lazy so far, and just said that a limit equals some value because it looked like it was going to.
That is not really good enough! Read more at Evaluating Limits.
Theorem1.3.1Basic Limit Properties
Let (btext{,}) (ctext{,}) (L) and (K) be real numbers, let (n) be a positive integer, and let (f) and (g) be functions with the following limits: begin{align*}lim_{xto c}f(x)amp=Lamplim_{xto c} g(x)amp = Ktext{.}end{align*}
The following limits hold.
(limlimits_{xto c} b = b)
(limlimits_{xto c} x = c)
1.3 Limits Graphical And Analytical Connectionsap Calculus Solutions
(limlimits_{xto c}(f(x)pm g(x)) = Lpm K)
(limlimits_{xto c}(bcdot f(x)) = bL)
(limlimits_{xto c} (f(x)cdot g(x)) = LK)

(limlimits_{xto c} (f(x)/g(x)) = L/Ktext{,}) when (Kneq 0)
(limlimits_{xto c} f(x)^n = L^n)
(limlimits_{xto c} sqrt[n]{f(x)} = sqrt[n]{L})
(If (n) is even, (L) must be non-negative.)
If either of the following holds:
(limlimits_{xto c}f(x)=Ltext{,}) (limlimits_{xto L}g(x)=Ktext{,}) and (g(L)=K)
(limlimits_{xto c}f(x)=Ltext{,}) (limlimits_{xto L}g(x)=Ktext{,}) and (f(x)neq L) for all (x) close to but not equal to (c)
then (limlimits_{xto c}g(f(x)) = Ktext{.})